2. Grundbegriffe
2.1. Wahrscheinlichkeitsfunktion f
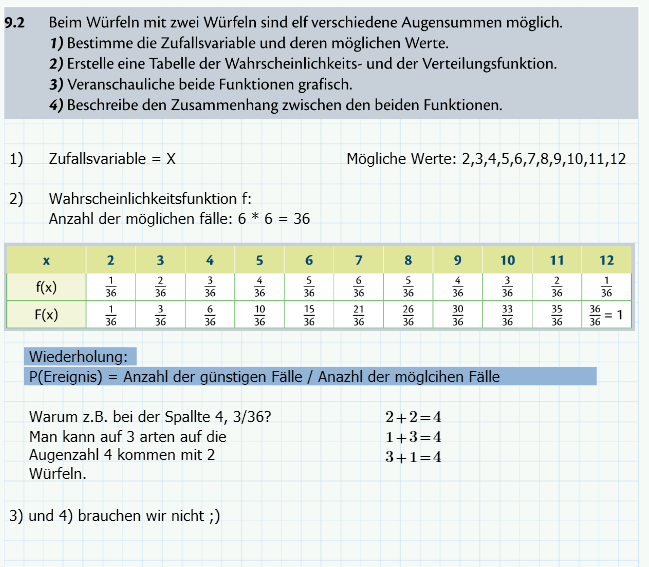
Die Wahrscheinlichkeitsfunktion f ordnet jedem Wert einer diskreten Zufallsvariablen X die Wahrscheinlichkeit zu, dass X genau diesen Wert annimmt:

Die Summe aller Funktionswerte von f ist 1.
2.2. Verteilungsfunktion F
Die Verteilungsfunktion F ordnet jedem Wert einer Diskreten Zufallsvariablen X die Wahrscheinlichkeit zu, dass X höchstens diesen Wert annimmt:
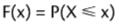
Sie ist also die Summe der Einzelwahrscheinlichkeit bis zu diesem Wert.